Atividade de Plano Cartesiano 6º e 7º Ano c/ Gabarito

O plano cartesiano é uma ferramenta essencial na matemática, permitindo a localização de pontos, a representação gráfica de funções e o desenvolvimento do pensamento espacial. Para auxiliar os professores no ensino desse tema, preparamos uma série de exercícios práticos para os alunos do 6º e 7º ano. As atividades envolvem identificação de coordenadas, plotagem de pontos e análise de gráficos, ajudando a consolidar esse conhecimento de forma clara e interativa.

---

Exercícios de Plano Cartesiano

1. Identificação de Coordenadas

Observe o plano cartesiano abaixo e escreva as coordenadas dos pontos A, B, C e D:

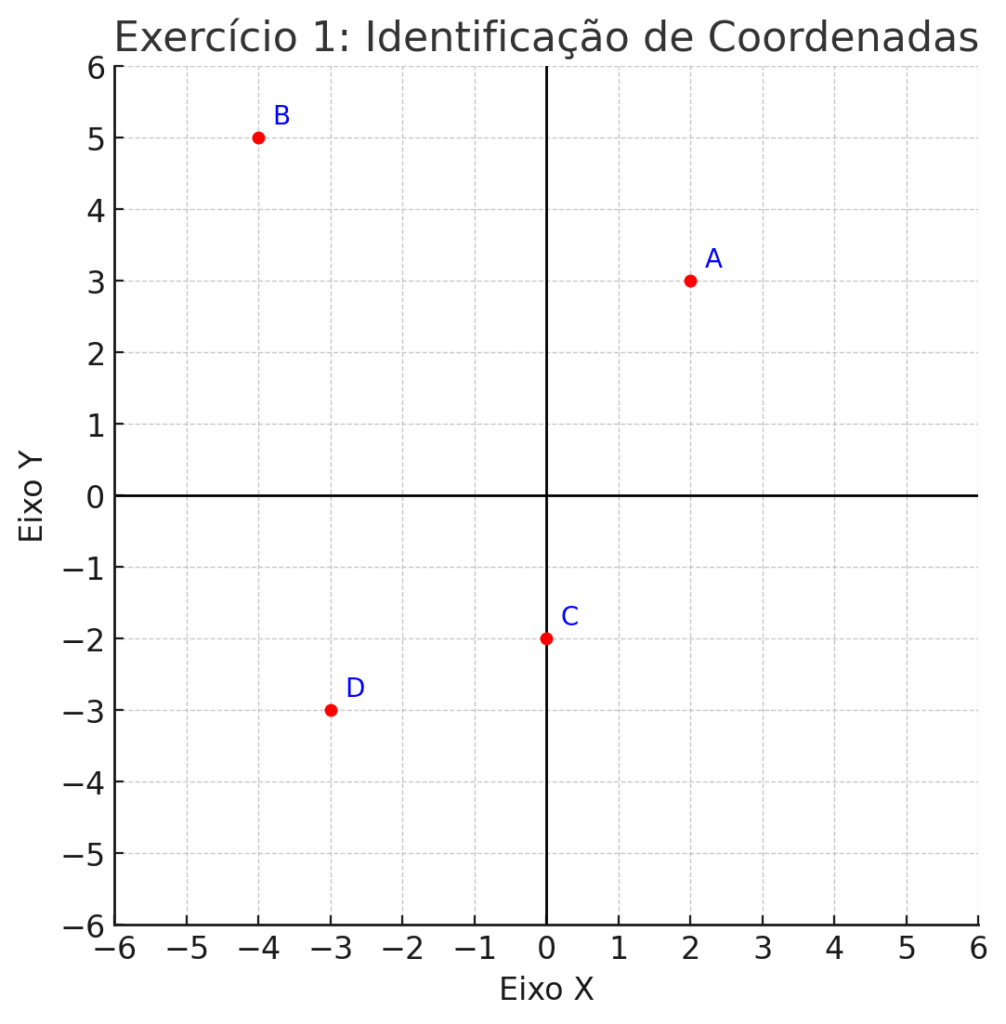
• A: (__, __)
• B: (__, __)
• C: (__, __)
• D: (__, __)

---

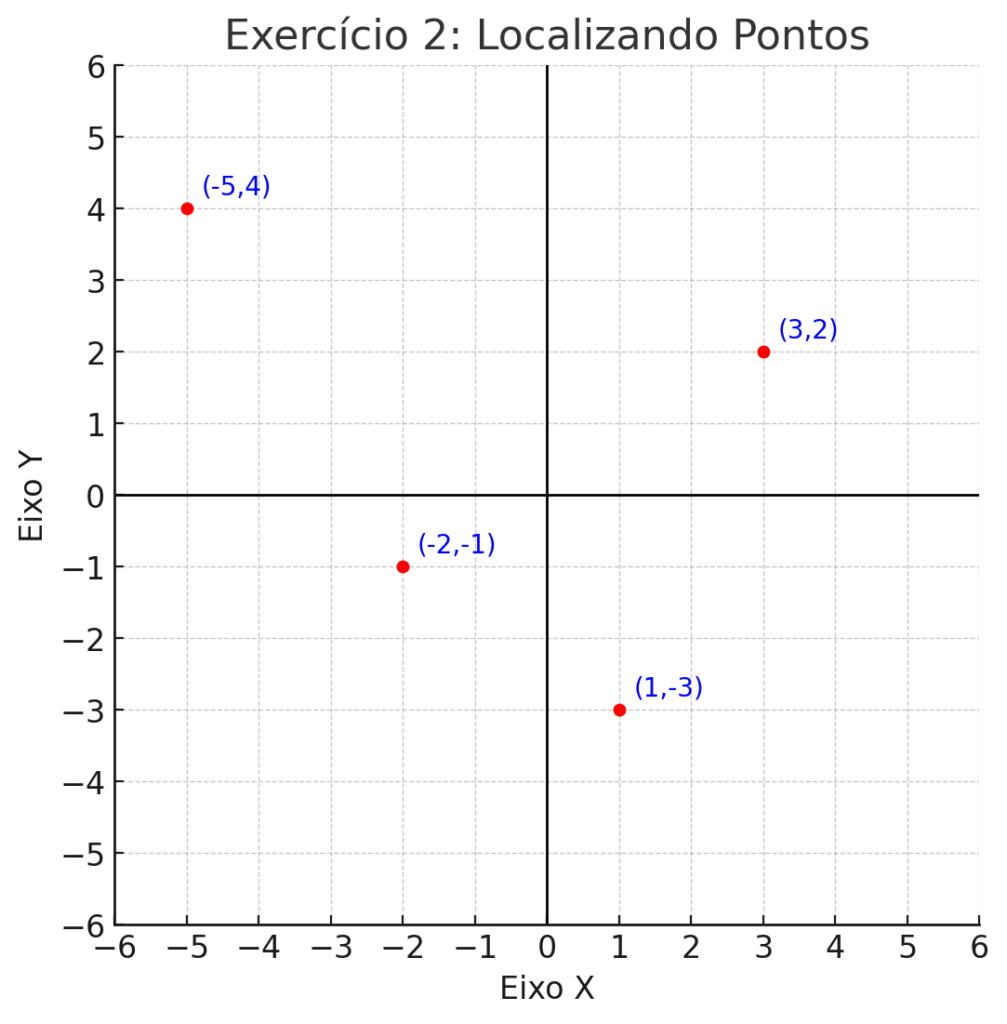
2. Localizando Pontos

No plano cartesiano, localize e marque os seguintes pontos:

• P (3,2)
• Q (-5,4)
• R (1,-3)
• S (-2,-1)

---

3. Quadrantes do Plano Cartesiano

Determine em qual quadrante cada um dos pontos abaixo se encontra:

• (5, 7) → ____
• (-6, 2) → ____
• (-3, -8) → ____
• (0, -4) → ____

---

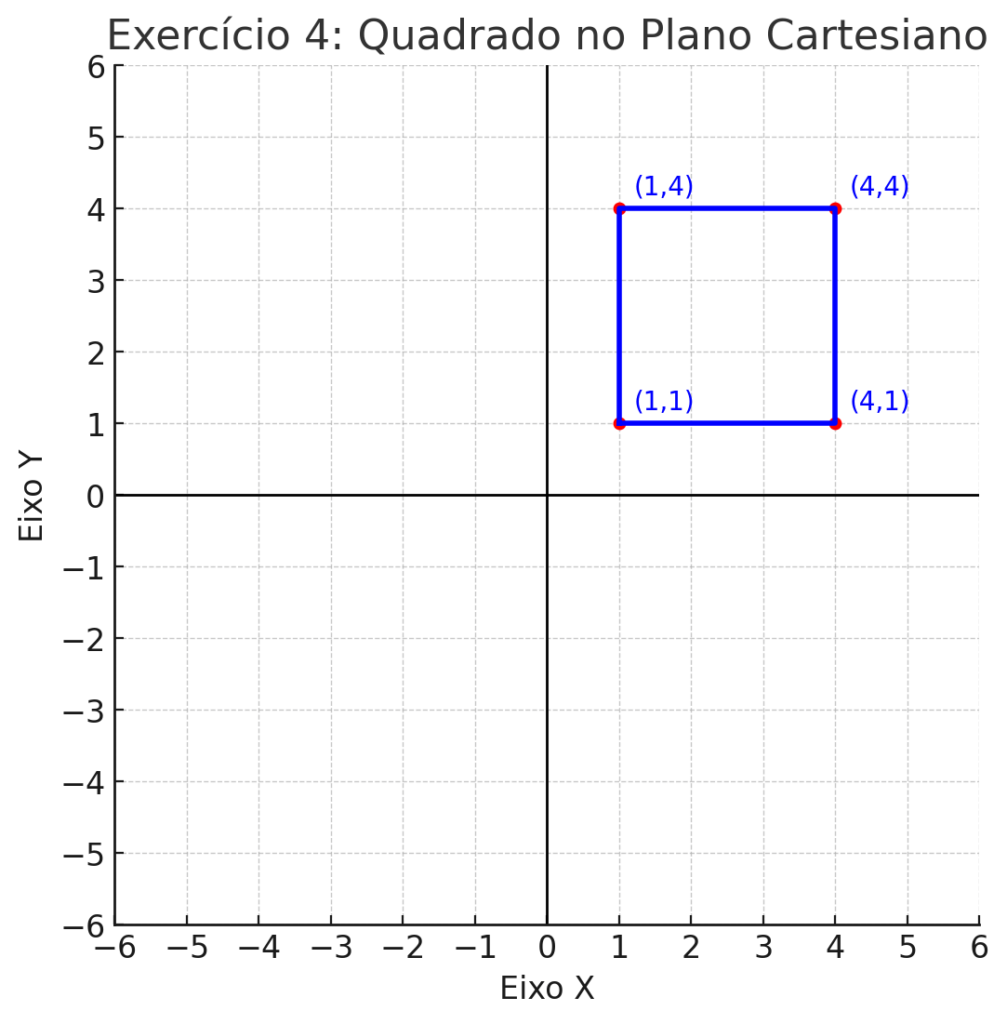
4. Desenhando no Plano Cartesiano

Marque os seguintes pontos no plano cartesiano e descubra qual figura geométrica eles formam:

• A (1,1)
• B (1,4)
• C (4,4)
• D (4,1)

Qual figura foi formada? _______________

---

5. Distância entre Dois Pontos

Calcule a distância entre os pontos dados:

• (2,3) e (2,7)
• (-4,-1) e (-4,3)
• (0,5) e (0,-2)

---

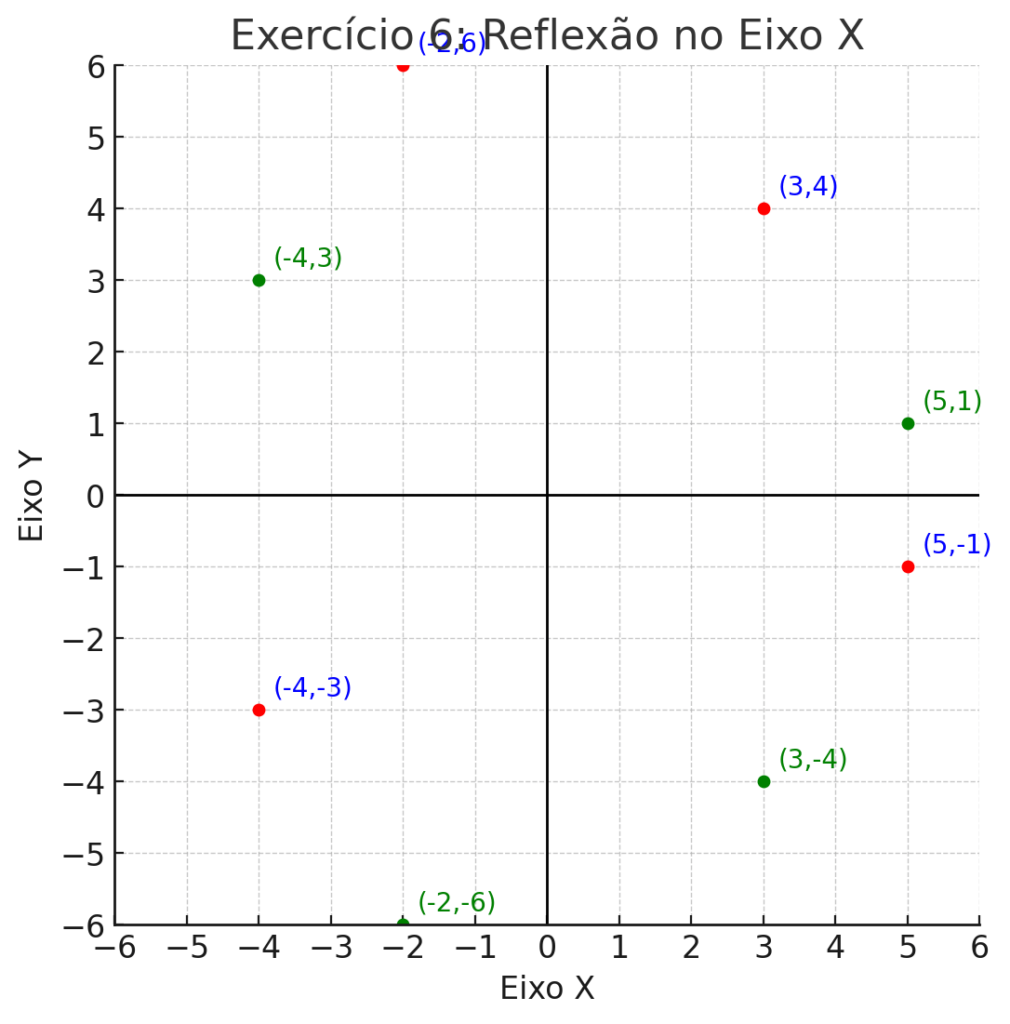
6. Espelhamento no Eixo X

Os pontos abaixo foram refletidos no eixo X. Determine as novas coordenadas:

• (3,4) → ____
• (-2,6) → ____
• (5,-1) → ____
• (-4,-3) → ____

---

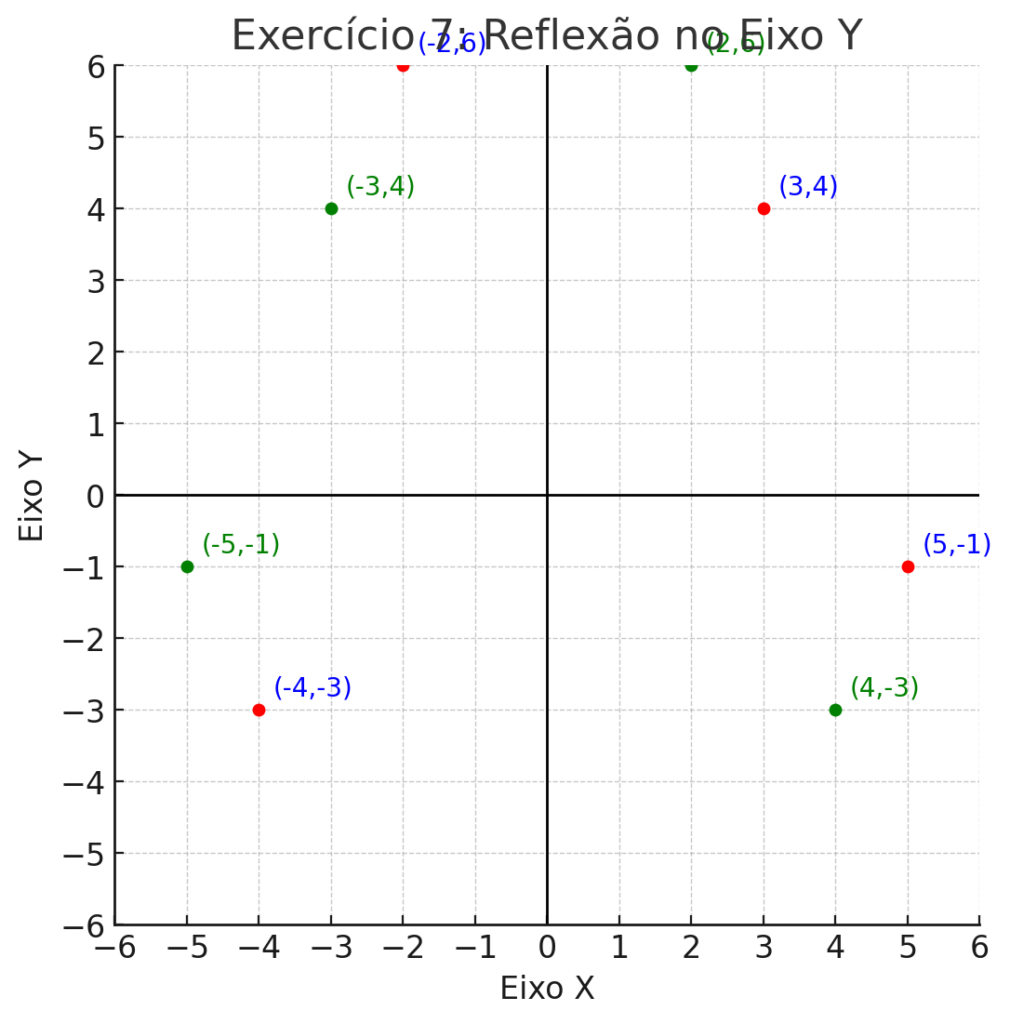
7. Espelhamento no Eixo Y

Os pontos abaixo foram refletidos no eixo Y. Determine as novas coordenadas:

• (3,4) → ____
• (-2,6) → ____
• (5,-1) → ____
• (-4,-3) → ____

---

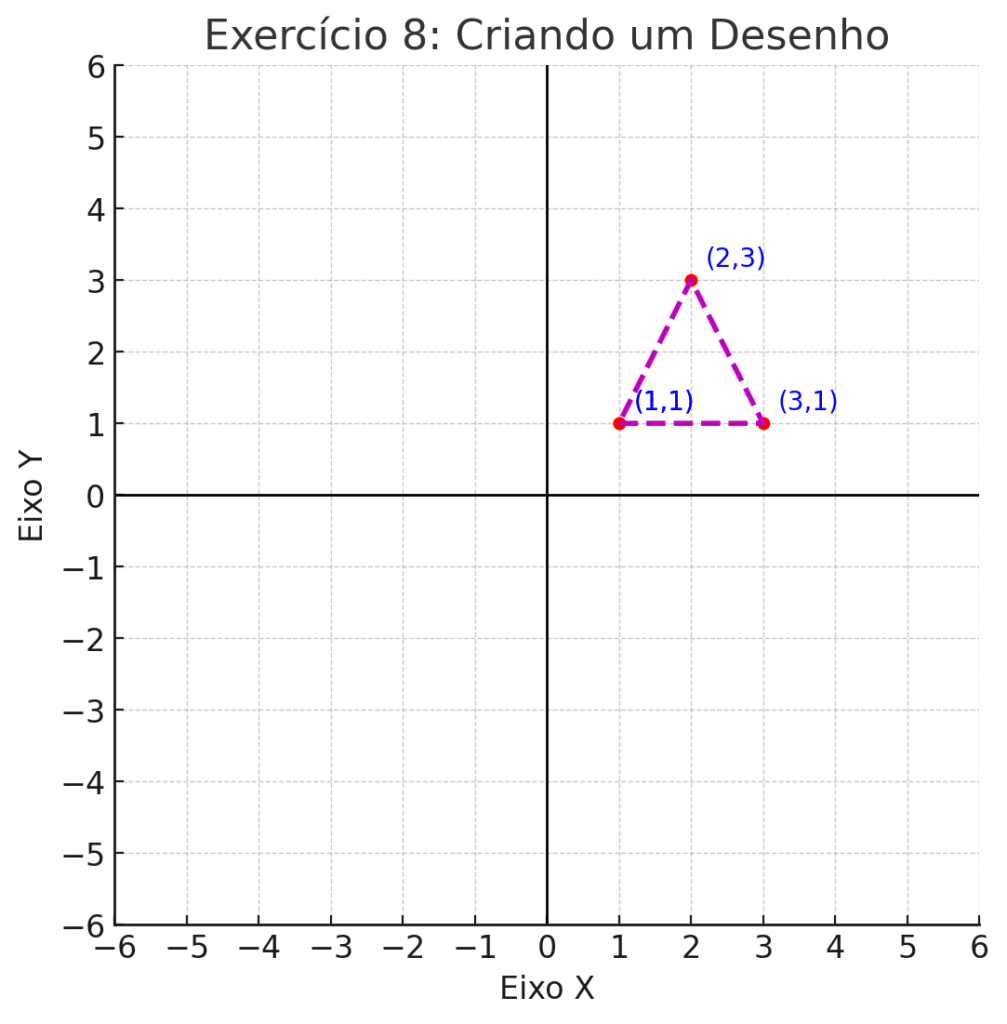
8. Criando um Desenho

Plote os seguintes pontos no plano cartesiano e descubra qual imagem é formada:

• A (1,1)
• B (3,1)
• C (2,3)
• D (1,1)

---

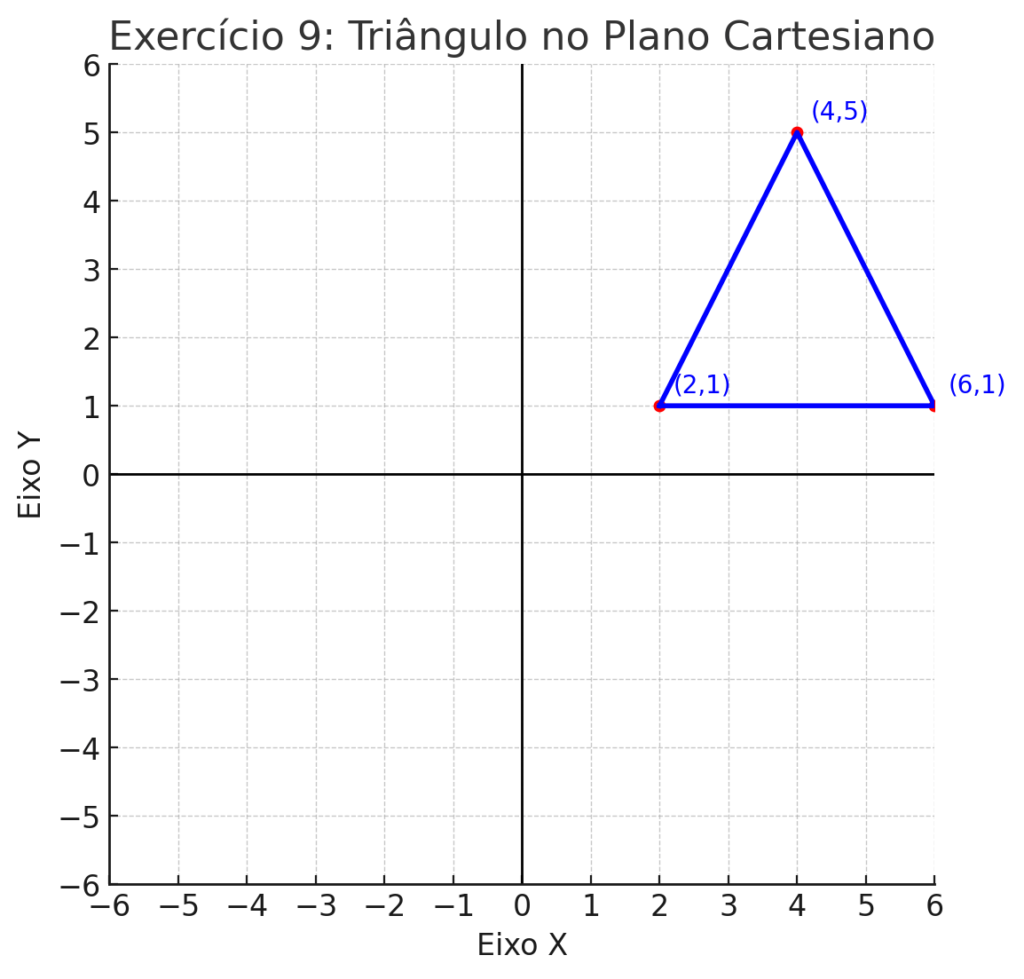
9. Coordenadas de um Triângulo

Dado o triângulo com vértices nos pontos (2,1), (6,1) e (4,5), determine:

• A base do triângulo mede quantas unidades? ____
• A altura do triângulo mede quantas unidades? ____

---

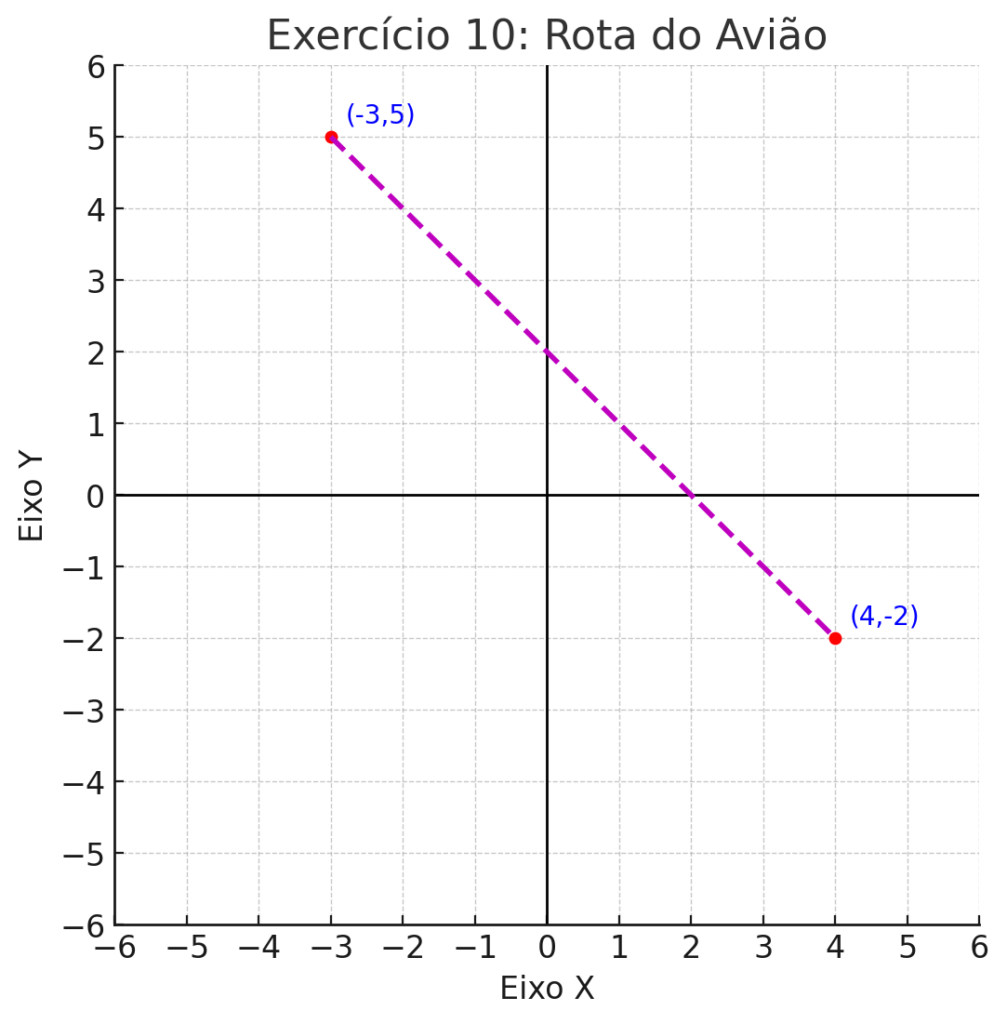
10. Problema do Avião

Um avião está voando no ponto (-3,5) do plano cartesiano. Ele precisa pousar no ponto (4,-2). Se cada unidade do plano representa 1 km, qual a distância que ele precisa percorrer?

---

Gabarito

1. A:(2,3); B:(-4,5); C:(0,-2); D:(-3,-3)

2.

3. Quadrantes:
   • (5,7) → 1º quadrante
   • (-6,2) → 2º quadrante
   • (-3,-8) → 3º quadrante
   • (0,-4) → Eixo Y (não está em um quadrante específico)
4. Figura formada: quadrado.

5. Distâncias:
   • (2,3) e (2,7) → 4 unidades
   • (-4,-1) e (-4,3) → 4 unidades
   • (0,5) e (0,-2) → 7 unidades
6. Espelhamento no eixo X:
   • (3,4) → (3,-4)
   • (-2,6) → (-2,-6)
   • (5,-1) → (5,1)
   • (-4,-3) → (-4,3)

7. Espelhamento no eixo Y:
   • (3,4) → (-3,4)
   • (-2,6) → (2,6)
   • (5,-1) → (-5,-1)
   • (-4,-3) → (4,-3)

8. Imagem formada: Triângulo.

9. Base do triângulo: 4 unidades. Altura: 4 unidades.

10. Distância percorrida pelo avião (usando Teorema de Pitágoras):

Para calcular a distância entre os pontos (-3,5) e (4,-2), utilizamos a fórmula da distância entre dois pontos no plano cartesiano:

Fórmula:
d = √((x₂ – x₁)² + (y₂ – y₁)²)

Substituindo os valores:
d = √((4 – (-3))² + (-2 – 5)²)
d = √((4 + 3)² + (-2 – 5)²)
d = √(7² + (-7)²)
d = √(49 + 49)
d = √98
d ≈ 9,9

Portanto, a distância percorrida pelo avião é de aproximadamente 9,9 km.

---

Atividade de Plano Cartesiano em PDF

Conclusão

Esses exercícios foram elaborados para proporcionar uma abordagem prática do plano cartesiano para alunos do 6º e 7º ano. Com atividades de localização, espelhamento e problemas aplicados, os estudantes poderão compreender melhor os conceitos essenciais dessa ferramenta matemática. Professores podem utilizar esse material como base para aulas dinâmicas e interativas, incentivando a participação e a resolução de desafios matemáticos.

Veja mais Atividades de Matemática para 6º Ano

Veja mais Atividades de Matemática para 7º Ano