Atividade sobre Bissetriz e Mediatriz para 8º e 9º Ano

As construções geométricas são fundamentais para compreender as propriedades das figuras planas e suas relações. Entre as construções mais importantes estão a bissetriz e a mediatriz, que aparecem em diversos contextos da matemática, da engenharia e até do cotidiano.

Nesta atividade, os alunos irão explorar o que são, como se constroem e onde se aplicam essas duas retas especiais — a bissetriz, que divide um ângulo em duas partes iguais, e a mediatriz, que divide um segmento de reta ao meio e forma com ele um ângulo reto.

---

Parte teórica: Conceitos e Construções

1. Bissetriz de um ângulo
A bissetriz é a semirreta que parte do vértice de um ângulo e o divide em dois ângulos congruentes, ou seja, de mesma medida.
Para construí-la com régua e compasso:

1. Marque o vértice do ângulo e trace um arco que intersecte os dois lados do ângulo em pontos A e B.
2. Com o mesmo raio, trace dois arcos — um com centro em A e outro com centro em B — que se cruzem em um ponto C.
3. A semirreta que une o vértice ao ponto C é a bissetriz.

Aplicação prática:
A bissetriz é muito usada para encontrar o ponto equidistante dos lados de um ângulo, importante em construções arquitetônicas e na determinação de locais ideais (por exemplo, o ponto que fica à mesma distância de duas ruas que formam um cruzamento).

---

2. Mediatriz de um segmento
A mediatriz é a reta perpendicular a um segmento e que passa pelo seu ponto médio.
Para construí-la:

1. Dado o segmento AB, abra o compasso com uma abertura maior que a metade do segmento.
2. Com centro em A, trace um arco acima e outro abaixo do segmento.
3. Repita o processo com centro em B, obtendo dois pontos de interseção entre os arcos.
4. Ligue esses pontos: essa é a mediatriz do segmento AB.

Aplicação prática:
A mediatriz é muito utilizada para determinar o ponto equidistante entre dois locais, como o ponto ideal para construir uma torre de comunicação entre duas cidades.

---

Exercícios

1. Um ângulo é formado pelos lados de um muro e de uma cerca. Se a bissetriz desse ângulo for traçada, o que ela representa em relação a esses dois elementos?

a) A linha mais distante entre eles
b) A linha que divide o ângulo em duas partes iguais
c) A linha perpendicular aos dois lados
d) A linha que passa pelo ponto médio do muro

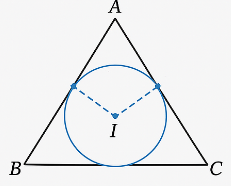
2. Em uma praça em formato de um triângulo equilátero, os jardineiros querem colocar um chafariz no ponto que fique à mesma distância dos três lados. Em que ponto da figura ele deve ser colocado?
a) Na mediatriz
b) No baricentro
c) No incentro
d) No circuncentro

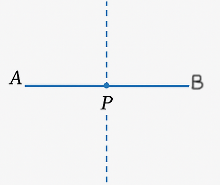
3. João traçou a mediatriz de um segmento AB. Se o ponto P pertence a essa mediatriz, o que se pode afirmar sobre as distâncias de P a A e B?
a) PA = PB
b) PA > PB
c) PA < PB
d) PA + PB = AB

4. Uma rua corta outra formando um ângulo de 60°. O engenheiro precisa instalar um poste de iluminação que fique exatamente no meio desse ângulo. Qual construção geométrica ele deve utilizar?
a) Mediatriz
b) Paralela
c) Bissetriz
d) Tangente

5. Dado um triângulo ABC, foram traçadas as bissetrizes de seus ângulos internos. O ponto onde elas se encontram é chamado de:
a) Baricentro
b) Incentro
c) Ortocentro
d) Circuncentro

6. A mediatriz dos lados de um triângulo se cruzam em um ponto chamado circuncentro. O que esse ponto representa?

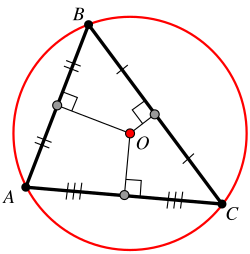
a) O centro do círculo inscrito
b) O centro do círculo circunscrito
c) O ponto médio da base
d) O vértice do ângulo maior

7. Em uma atividade prática, um aluno marcou dois pontos A e B representando duas cidades. Ele quer construir uma estrada que passe exatamente no ponto equidistante das duas. Qual construção geométrica ele deve usar?
a) Traçar a mediatriz de AB
b) Traçar a bissetriz do ângulo formado entre as cidades
c) Traçar uma reta paralela a AB
d) Traçar uma perpendicular em A

8. Uma arquiteta precisa cortar um ângulo de 80° em duas partes para desenhar um projeto simétrico. Qual será a medida de cada parte após traçar a bissetriz?
a) 20°
b) 30°
c) 40°
d) 50°

9. Durante um exercício de geometria, a professora pediu que os alunos construíssem a mediatriz de um segmento de 10 cm. Qual é a distância do ponto médio até cada extremidade do segmento?
a) 2 cm
b) 4 cm
c) 5 cm
d) 10 cm

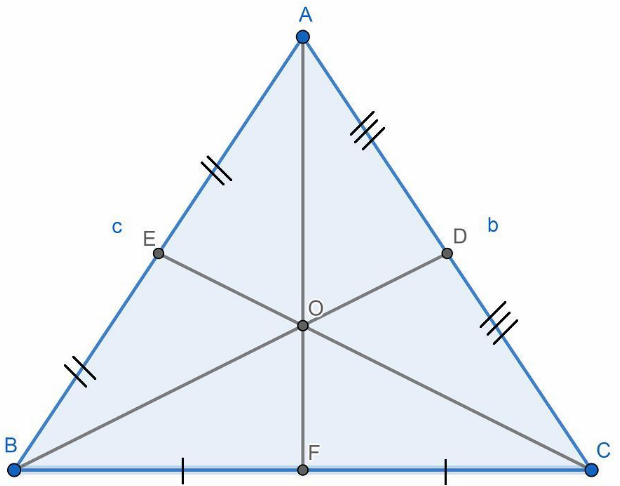
10. No triângulo ABC, as mediatrizes dos lados se encontram no ponto O, e as bissetrizes dos ângulos se encontram no ponto I. Que diferença prática há entre os pontos O e I? Explique em poucas palavras.

---

Gabarito

1. b
2. c
   

3. a

4. c
5. b

6. b
7. a
8. c
9. c
10. O ponto O é o circuncentro, centro da circunferência que passa pelos vértices do triângulo. Já o ponto I é o incentro, centro da circunferência que toca internamente os lados do triângulo.

---

Conclusão

O estudo da bissetriz e da mediatriz é essencial para o desenvolvimento do raciocínio geométrico e para a compreensão espacial dos alunos. Além de reforçar a importância da precisão e da simetria, essas construções aproximam a matemática da realidade, mostrando como ela é aplicada em engenharia, arquitetura e design.

Sugere-se que o professor complemente esta atividade com aulas práticas usando régua e compasso, ou ainda, com softwares de geometria dinâmica, como o GeoGebra, para consolidar a compreensão dos alunos sobre as propriedades dessas construções.

Veja mais Atividades de Matemática para 8º Ano

Veja mais Atividades de Matemática para 9º Ano