A função afim é um dos temas mais importantes da matemática no 9º ano, sendo essencial para desenvolver o raciocínio lógico e a resolução de problemas. Nesta postagem, apresentamos 12 exercícios variados sobre o tema, abordando tanto a teoria quanto aplicações práticas. O material também inclui o gabarito para facilitar o acompanhamento. Perfeito para os professores utilizarem em sala de aula ou adaptarem às suas necessidades.
✏️ Pacote de Atividades de Matemática do 6º ao 9º Ano
✔Atividades em Word ✔Editáveis ✔Com Gabarito ✔Alinhadas à BNCC
Já ajudou + de 1.000 Educadores a economizar horas de planejamento.
Quero Conhecer o Pacote!Garantia de satisfação de 7 dias
Preparação para a aula
Antes de aplicar os exercícios, revisite com os alunos os conceitos básicos da função afim:
- A função afim é definida pela fórmula f(x) = ax + b, onde:
- a é o coeficiente angular, que indica a inclinação da reta;
- b é o coeficiente linear, que indica onde a reta corta o eixo y.
- Se o valor de a for positivo, a função é crescente; se for negativo, a função é decrescente.
- Use exemplos do cotidiano, como custos fixos e variáveis, para tornar o conteúdo mais próximo da realidade dos alunos.
1ª Lista de Exercícios sobre Função Afim para o 9º Ano
- Identifique os valores de a e b na função f(x) = 3x – 5.
- Calcule o valor de f(2) para a função f(x) = -2x + 4.
- Determine a raiz da função f(x) = 5x – 10 (o valor de x para o qual f(x) = 0).
- Esboce o gráfico da função f(x) = 2x + 1 e indique os pontos de interseção com os eixos x e y.
- Uma empresa cobra R$ 50 fixos mais R$ 20 por hora de trabalho. Escreva a função que representa o custo total C(h) e calcule o valor de C(3), quando o número de horas trabalhadas é 3.
- Classifique as funções abaixo como crescentes ou decrescentes:
a) f(x) = -4x + 7
b) f(x) = 2x – 1
c) f(x) = 0,5x + 3 - Resolva: se f(x) = 3x + 2, encontre o valor de x para o qual f(x) = 11.
- Uma loja oferece um desconto de R$ 5 para cada R$ 100 de compras, além de uma taxa fixa de R$ 20. Escreva a função que representa o custo final de uma compra e determine o custo para uma compra de R$ 300.
- Verifique se o ponto (2, 4) pertence à função f(x) = 2x.
- Se f(x) = 4x – 6, qual o valor de f(-1)?
- Uma piscina perde 10 litros de água por dia devido à evaporação. Sabendo que ela começa com 5000 litros, escreva a função que representa o volume de água na piscina ao longo dos dias. Qual será o volume após 15 dias?
- Uma linha reta passa pelos pontos (0, 2) e (4, 10). Determine a equação da função afim correspondente.
Gabarito com Resolução da 1º Lista de Exercícios
1. Identifique os valores de a e b na função f(x) = 3x – 5.
- a = 3 (coeficiente de x)
- b = -5 (termo independente)
Resposta: a = 3; b = -5.
2. Calcule o valor de f(2) para a função f(x) = -2x + 4.
Substituímos x por 2:
f(2) = -2(2) + 4
f(2) = -4 + 4
f(2) = 0
Resposta: f(2) = 0.
3. Determine a raiz da função f(x) = 5x – 10.
Para encontrar a raiz, fazemos f(x) = 0:
0 = 5x – 10
5x = 10
x = 10/5
x = 2
Resposta: x = 2.
4. Esboce o gráfico da função f(x) = 2x + 1.
Para encontrar os pontos de interseção:
- Quando x = 0, f(0) = 2(0) + 1 = 1 (interseção com o eixo y).
- Quando f(x) = 0, 0 = 2x + 1 → x = -1/2 (interseção com o eixo x).
Pontos principais: (0, 1) e (-0,5, 0).
Resposta: Pontos principais (0, 1) e (-0,5, 0).
5. Escreva a função que representa o custo total C(h) e calcule o valor de C(3).
A função é C(h) = 20h + 50.
Para h = 3:
C(3) = 20(3) + 50
C(3) = 60 + 50
C(3) = 110
Resposta: C(h) = 20h + 50; C(3) = 110.
6. Classifique as funções abaixo como crescentes ou decrescentes:
a) f(x) = -4x + 7 → decrescente (a < 0)
b) f(x) = 2x – 1 → crescente (a > 0)
c) f(x) = 0,5x + 3 → crescente (a > 0)
Resposta:
a) Decrescente
b) Crescente
c) Crescente
7. Resolva: se f(x) = 3x + 2, encontre o valor de x para o qual f(x) = 11.
11 = 3x + 2
3x = 11 – 2
3x = 9
x = 9/3
x = 3
Resposta: x = 3.
8. Escreva a função e determine o custo para uma compra de R$ 300.
A função é: C(x) = x – 5(x/100) + 20.
Para x = 300:
C(300) = 300 – 5(300/100) + 20
C(300) = 300 – 15 + 20
C(300) = 305
Resposta: Custo final = 305.
9. Verifique se o ponto (2, 4) pertence à função f(x) = 2x.
Substituímos x = 2 na função:
f(2) = 2(2) = 4
Como f(2) = 4, o ponto pertence à função.
Resposta: Sim, o ponto pertence à função.
10. Qual o valor de f(-1) na função f(x) = 4x – 6?
Substituímos x por -1:
f(-1) = 4(-1) – 6
f(-1) = -4 – 6
f(-1) = -10
Resposta: f(-1) = -10.
11. Escreva a função que representa o volume da piscina e determine o volume após 15 dias.
A função é V(t) = 5000 – 10t.
Para t = 15:
V(15) = 5000 – 10(15)
V(15) = 5000 – 150
V(15) = 4850
Resposta: V(t) = 5000 – 10t; volume final = 4850 litros.
12. Determine a equação da função que passa pelos pontos (0, 2) e (4, 10).
Coeficiente angular: a = (y2 – y1) / (x2 – x1)
a = (10 – 2) / (4 – 0)
a = 8 / 4
a = 2
A equação é f(x) = 2x + b.
Para determinar b, substituímos o ponto (0, 2):
2 = 2(0) + b
b = 2
Equação final: f(x) = 2x + 2
Resposta: f(x) = 2x + 2.
- a = 3; b = -5
- f(2) = -4
- x = 2
- Gráfico com pontos (0, 1) e (-0,5, 0)
- C(h) = 20h + 50; C(3) = 110
- a) Decrescente
b) Crescente
c) Crescente - x = 3
- Custo final = 295
- Sim, o ponto pertence à função.
- f(-1) = -10
- Volume final = 3500 litros
- f(x) = 2x + 2
1º Atividade de Função Afim em PDF
2ª Lista de Exercícios sobre Função do 1º Grau
Exercício 1 – Determine se as funções abaixo são crescentes, decrescentes ou constantes:
a) f(x) = 5x + 2
b) f(x) = -3x + 4
c) f(x) = 0x + 7
d) f(x) = -x – 5
e) f(x) = 2x – 10
Exercício 2 – Calcule o valor da função para os valores indicados:
a) f(x) = 3x + 1, para x = 4
b) f(x) = -2x + 5, para x = -3
c) f(x) = 4x – 8, para x = 0
d) f(x) = 5x + 9, para x = 2
e) f(x) = -x + 10, para x = 7
Exercício 3 – Em uma lanchonete, o preço de um lanche é composto por uma taxa fixa de R$5,00 mais R$3,00 por cada unidade pedida.
a) Monte a função que relaciona o preço total (P) com a quantidade de lanches (x).
b) Qual será o valor pago por 4 lanches?
c) Se a pessoa pagar R$26, quantos lanches comprou?
Exercício 4 – Uma empresa cobra um valor fixo de R$50,00 pelo serviço mais R$10,00 por hora trabalhada.
a) Escreva a função que representa o custo total C(x).
b) Quanto custará o serviço se forem trabalhadas 5 horas?
c) Quantas horas foram trabalhadas se o total pago foi R$120?
Exercício 5 – Calcule o valor de x quando f(x) = 0 nas seguintes funções:
a) f(x) = 2x – 6
b) f(x) = -4x + 8
c) f(x) = 5x + 15
d) f(x) = -x – 3
e) f(x) = 3x – 9
Exercício 6 – Analise os gráficos abaixo e diga, em cada caso, se a função é crescente ou decrescente, e o valor aproximado de a e b.
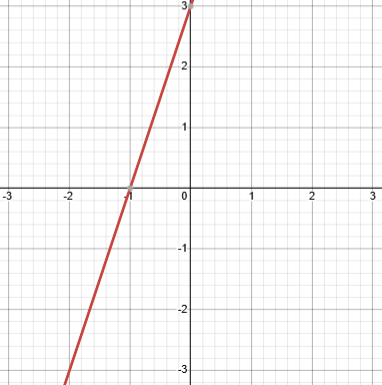
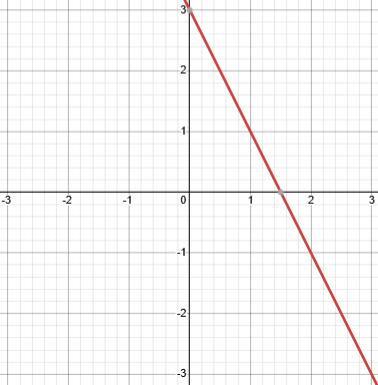
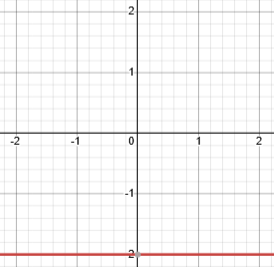
Exercício 7 – A função que representa o salário de um vendedor é S(x) = 1200 + 200x, em que x é o número de produtos vendidos.
a) Qual é o salário fixo do vendedor?
b) Quanto ele ganha por produto vendido?
c) Qual será o salário se ele vender 10 produtos?
d) Quantos produtos precisa vender para ganhar R$3.000?
Exercício 8 – Em uma corrida de táxi, o preço é composto por uma taxa de R$6,00 mais R$2,50 por quilômetro rodado.
a) Monte a função do preço P(x).
b) Quanto custará uma corrida de 8 km?
c) Quantos quilômetros o táxi percorreu se o passageiro pagou R$31?
Exercício 9 – A temperatura de um corpo resfriando pode ser representada pela função T(x) = 80 – 5x, onde x é o tempo em minutos.
a) Qual é a temperatura inicial?
b) Qual será a temperatura após 4 minutos?
c) Depois de quantos minutos a temperatura chegará a 50°C?
Exercício 10 – Observe o gráfico (imagine uma reta que cruza o eixo y em 4 e passa pelo ponto (2, 8)).
a) Determine o coeficiente angular a.
b) Escreva a função f(x).
c) Qual é o valor de f(5)?
d) Em que ponto a reta corta o eixo x?
Exercício 11 – A produção de uma fábrica é dada pela função P(x) = 200x + 1500, onde x é o número de dias.
a) Quantas unidades havia no início?
b) Quantas unidades serão produzidas em 10 dias?
c) Após quantos dias a produção total será de 3500 unidades?
Exercício 12 – Um carro se desloca segundo a função S(x) = 60x + 100, onde S é a posição (em km) e x é o tempo (em horas).
a) Qual era a posição inicial do carro?
b) Qual é a velocidade do carro?
c) Qual será sua posição após 3 horas?
d) Em que tempo o carro atingirá 400 km?
Exercício 13 – Determine a função do 1º grau que passa pelos pontos (0, 3) e (4, 11).
Exercício 14 – Um cano perde água a uma taxa constante, e a quantidade restante é dada por f(x) = 100 – 4x, onde x é o tempo em horas.
a) Qual é a quantidade inicial de água?
b) Qual será a quantidade após 6 horas?
c) Depois de quanto tempo a água acabará?
Exercício 15 – Uma empresa de telefonia cobra uma taxa mensal de R$30,00 mais R$0,50 por minuto utilizado. Outra empresa cobra R$40,00 mais R$0,30 por minuto.
a) Escreva as funções de custo A(x) e B(x) para cada empresa.
b) A partir de quantos minutos as duas empresas terão o mesmo custo?
c) Qual empresa é mais vantajosa para quem fala pouco?
d) E para quem fala muito?
Gabarito da 2ª Lista de Exercício
Exercício 1
a) a = 5 → crescente
b) a = -3 → decrescente
c) a = 0 → constante
d) a = -1 → decrescente
e) a = 2 → crescente
Exercício 2
a) f(4) = 3(4) + 1 = 13
b) f(-3) = -2(-3) + 5 = 11
c) f(0) = 4(0) – 8 = -8
d) f(2) = 5(2) + 9 = 19
e) f(7) = -7 + 10 = 3
Exercício 3
a) P(x) = 3x + 5
b) P(4) = 3(4) + 5 = 17
c) 26 = 3x + 5 → x = 7 lanches
Exercício 4
a) C(x) = 10x + 50
b) C(5) = 10(5) + 50 = 100
c) 120 = 10x + 50 → x = 7 horas
Exercício 5
a) 0 = 2x – 6 → x = 3
b) 0 = -4x + 8 → x = 2
c) 0 = 5x + 15 → x = -3
d) 0 = -x – 3 → x = -3
e) 0 = 3x – 9 → x = 3
Exercícios 6
a) Crescente
b) Descrescente
c) Crescente
Exercício 7
a) Salário fixo: 1200
b) Comissão: 200
c) S(10) = 1200 + 200(10) = 3200
d) 3000 = 1200 + 200x → x = 9 produtos
Exercício 8
a) P(x) = 2,5x + 6
b) P(8) = 2,5(8) + 6 = 26
c) 31 = 2,5x + 6 → x = 10 km
Exercício 9
a) T(0) = 80 → temperatura inicial
b) T(4) = 80 – 5(4) = 60
c) 50 = 80 – 5x → x = 6 minutos
Exercício 10
a) Dois pontos: (0, 4) e (2, 8)
a = (8 – 4)/(2 – 0) = 2
b) f(x) = 2x + 4
c) f(5) = 2(5) + 4 = 14
d) 0 = 2x + 4 → x = -2
Exercício 11
a) 1500 unidades iniciais
b) P(10) = 200(10) + 1500 = 3500
c) 3500 = 200x + 1500 → x = 10 dias
Exercício 12
a) Posição inicial: 100 km
b) Velocidade: 60 km/h
c) S(3) = 60(3) + 100 = 280
d) 400 = 60x + 100 → x = 5 horas
Exercício 13
f(0) = 3 → b = 3
f(4) = 11 → 11 = 4a + 3 → a = 2
Função: f(x) = 2x + 3
Exercício 14
a) 100 litros iniciais
b) f(6) = 100 – 4(6) = 76
c) 0 = 100 – 4x → x = 25 horas
Exercício 15
a) A(x) = 0,5x + 30 e B(x) = 0,3x + 40
b) Igualando: 0,5x + 30 = 0,3x + 40
0,2x = 10 → x = 50 minutos
c) Para poucos minutos → empresa A (menor taxa fixa)
d) Para muitos minutos → empresa B (menor valor por minuto)
2ª Atividade de Função do 1º Grau em PDF
3ª Lista de Exercícios sobre Função Afim com Resolução
- Determine o valor de f(x), sabendo que f(x) = 3x + 2 e x = 4.
- Se f(x) = -2x + 5, calcule f(-3).
- Qual é o coeficiente angular da função f(x) = 7x – 4?
- Qual é o coeficiente linear da função f(x) = -5x + 9?
- A função f(x) = 4x – 12 corta o eixo y em qual ponto?
- Se a função é f(x) = kx + 3 e f(2) = 11, qual o valor de k?
- Uma função é dada por f(x) = 6x – 10. Calcule f(0).
- Ache a lei da função sabendo que f(2) = 8 e f(5) = 17.
- O gráfico da função f(x) = ax + b passa pelo ponto (0, -2). Qual é o valor de b?
- Diga se a função f(x) = -3x + 7 é crescente ou decrescente.
- Uma corrida de táxi custa R$ 5,00 mais R$ 2,50 por quilômetro rodado. Escreva a função que representa o valor V em função da distância d.
- Calcule o valor a pagar por 12 km percorridos na corrida do exercício anterior.
Gabarito da 3ª Lista de Exercícios
- f(4) = 3 × 4 + 2 = 14
- f(-3) = -2 × (-3) + 5 = 11
- 7
- 9
- No ponto (0, -12)
- k = (11 – 3) / 2 = 4
- f(0) = -10
- A inclinação é (17 – 8) / (5 – 2) = 3. Portanto, f(x) = 3x + 2.
- b = -2
- Decrescente (coeficiente angular negativo)
- V(d) = 2,50 × d + 5,00
- V(12) = 2,50 × 12 + 5 = 35,00 reais
3º Atividade de Função de 1º Grau em PDF
4ª Lista de Exercícios sobre Função de 1º Grau com Resolução
1. Determine o valor de f(4), sabendo que f(x) = 3x + 2.
Resolução:
Substituindo x por 4:
f(4) = 3 × 4 + 2
f(4) = 12 + 2
f(4) = 14
2. A função f(x) = -2x + 10 representa o custo para produzir x unidades de um produto. Qual é o custo para 3 unidades?
Resolução:
f(3) = -2 × 3 + 10
f(3) = -6 + 10
f(3) = 4
O custo é 4.
3. Encontre a raiz da função f(x) = 5x – 15.
Resolução:
A raiz ocorre quando f(x) = 0:
0 = 5x – 15
15 = 5x
x = 3
A raiz é x = 3.
4. A função que passa pelos pontos (0, 8) e (2, 4) é afim. Determine sua lei.
Resolução:
Coeficiente angular m:
m = (4 – 8) / (2 – 0)
m = -4 / 2
m = -2
Como passa pelo ponto (0, 8), o coeficiente b é 8.
Logo, f(x) = -2x + 8.
5. Uma corrida de táxi cobra tarifa inicial de 6 reais e mais 2 reais por quilômetro rodado. Escreva a função que relaciona o valor total ao número de quilômetros.
Resolução:
Tarifa inicial é b = 6
Preço por km é m = 2
Função: f(x) = 2x + 6
6. Para a função f(x) = 7 – x, determine f(-3).
Resolução:
f(-3) = 7 – (-3)
f(-3) = 7 + 3
f(-3) = 10
7. Determine o coeficiente angular e o coeficiente linear da função f(x) = 9x – 4.
Resolução:
m = 9
b = -4
8. A altura de uma planta, em cm, pode ser aproximada por h(x) = 2x + 5, onde x é o número de semanas. Qual será a altura após 10 semanas?
Resolução:
h(10) = 2 × 10 + 5
h(10) = 20 + 5
h(10) = 25 cm
9. Determine a imagem de x = 1 na função f(x) = -5x + 7.
Resolução:
f(1) = -5 × 1 + 7
f(1) = -5 + 7
f(1) = 2
10. Uma função afim tem coeficiente angular 3 e passa pelo ponto (2, 1). Determine sua lei.
Resolução:
Se f(x) = 3x + b, substituímos o ponto:
1 = 3 × 2 + b
1 = 6 + b
b = -5
Função: f(x) = 3x – 5
Conclusão
A função afim é um conteúdo que conecta conceitos matemáticos a situações práticas do dia a dia, tornando a aula mais interessante e significativa. Esperamos que estas atividades auxiliem no aprendizado de seus alunos e que os exercícios possam ser aplicados com facilidade em sala de aula.
Veja também: Função Afim: Entenda tudo sobre a Função de 1º Grau
Veja também: Mais Exercícios de Matemática para 9º Ano
📘 Gostou da Atividade?
Essa foi apenas uma amostra!
✅ Quero o Pacote Completo!📥 Acesso imediato em minutos após o pagamento





