Exercícios de Função Quadrática 9º Ano com Gabarito

As funções quadráticas desempenham um papel fundamental no ensino da matemática, especialmente no 9º ano. Elas são usadas para resolver problemas envolvendo trajetórias, maximização e minimização de valores e muito mais. Neste post, você encontrará uma seleção de 10 exercícios de função quadrática acompanhados de gabarito. Os exercícios foram elaborados para ajudar professores a inspirarem ou aplicarem diretamente em sala de aula, com exemplos que incluem gráficos para uma melhor compreensão visual do tema.

---

Exercícios de Função Quadrática

1. A função f(x) = -2x² + 4x + 6 representa uma parábola.
   Determine a concavidade e o valor do coeficiente a.

---

2. Determine as raízes da função f(x) = x² – 5x + 6 utilizando o método da fatoração.

---

3. A função f(x) = 3x² – 6x + 4 está dada.
   Calcule as coordenadas do vértice dessa parábola.

---

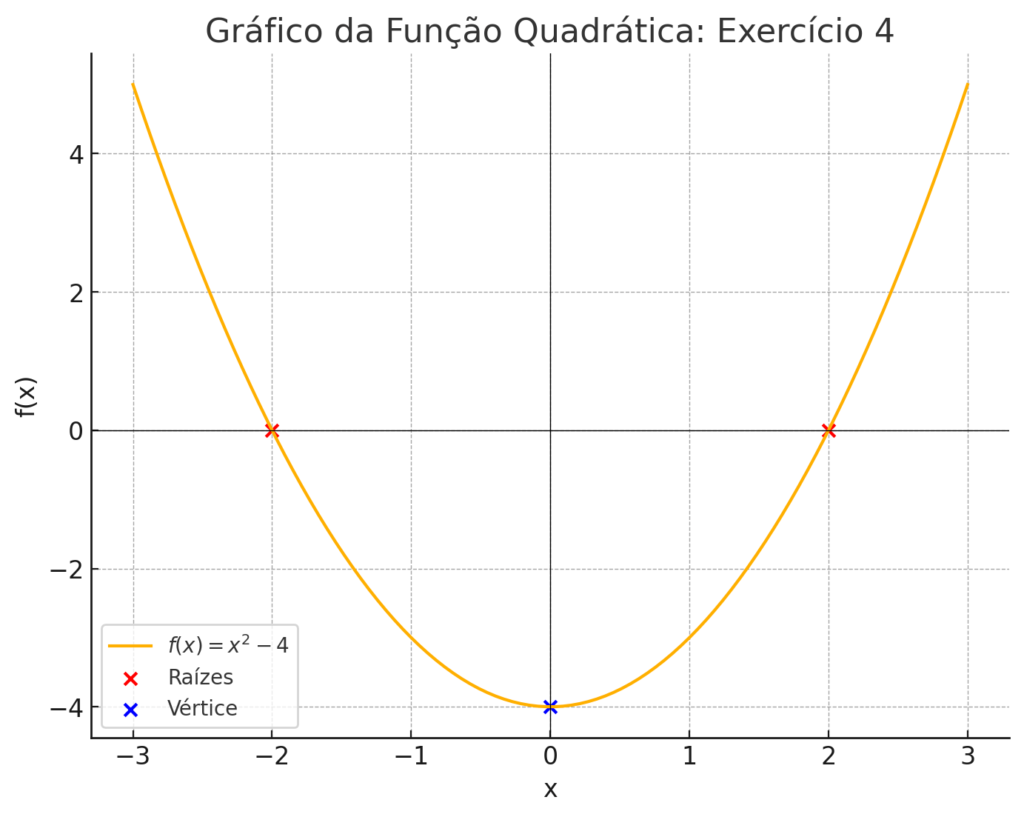
4. Considere a função f(x) = x² – 4.
   Esboce o gráfico dessa função, indicando as raízes, o vértice e o eixo de simetria.

---

5. A função f(x) = -x² + 4x – 3 é dada.
   Determine se a função possui valor máximo ou mínimo e calcule esse valor.

---

6. Um projétil é lançado e sua altura é dada pela função h(t) = -5t² + 20t, onde h(t) é a altura em metros e t é o tempo em segundos.
   Qual é a altura máxima atingida pelo projétil e em que momento isso ocorre?

---

7. Dada a função f(x) = 2x² – 8x + 5:
   a) Identifique os coeficientes a, b e c.
   b) Explique o efeito do sinal de a na concavidade da parábola.

---

8. Para a função f(x) = x² – 7x + 10:
   a) Determine as raízes.
   b) Verifique se a soma e o produto das raízes correspondem às relações -b/a e c/a.

---

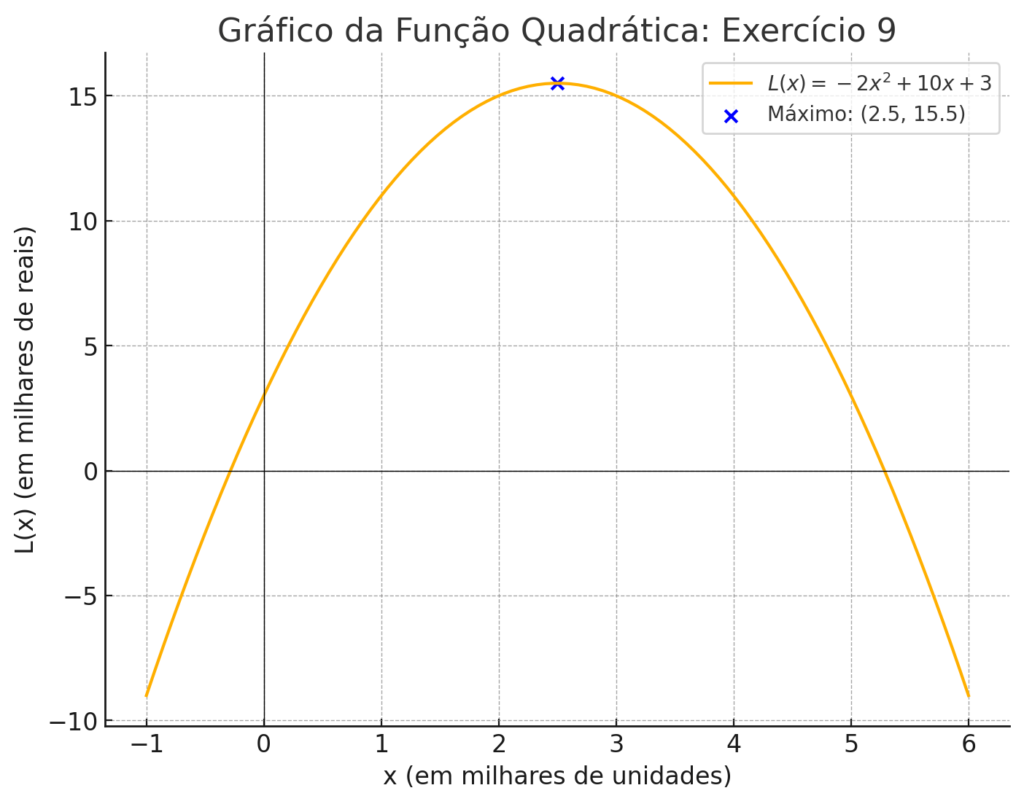
9. Um empresário quer modelar o lucro L(x) de sua empresa pela função L(x) = -2x² + 10x + 3, onde x é o número de unidades produzidas (em milhares).
   Qual é o número ideal de unidades para maximizar o lucro e qual é o lucro máximo?

---

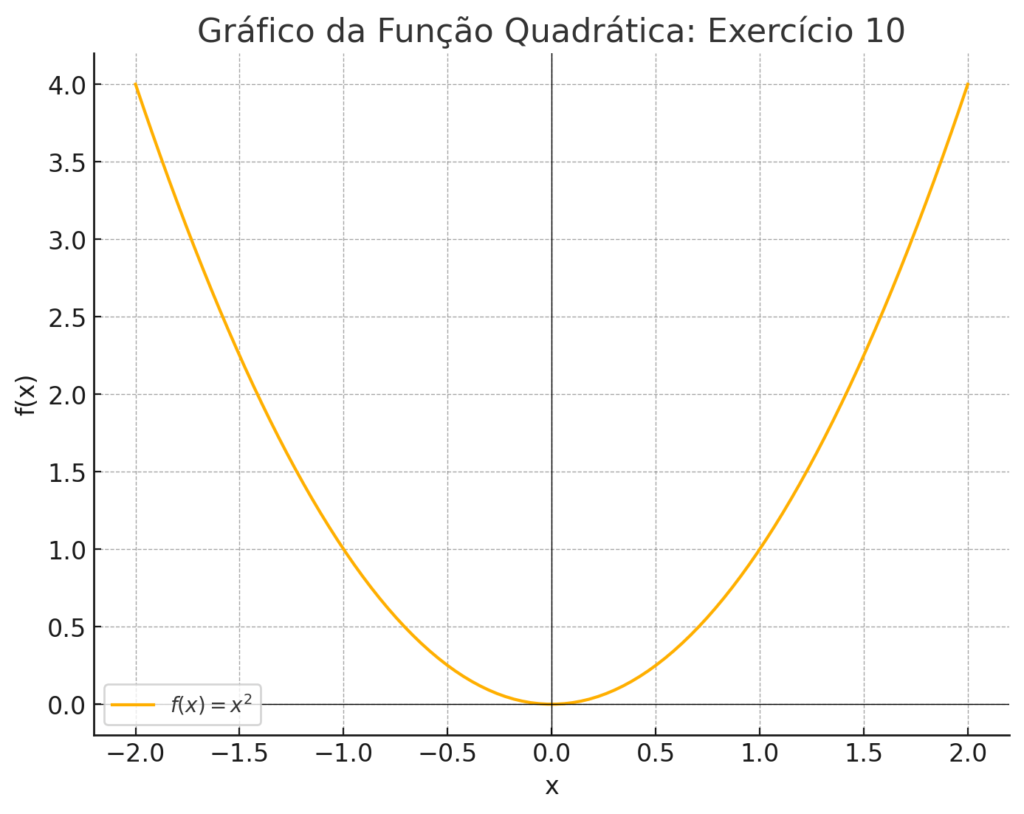
10. Analise o gráfico da função f(x) = x². Qual é o domínio e a imagem da função?

---

Gabarito

1. A concavidade é voltada para baixo (a < 0). Coeficiente a = -2.
2. Raízes: x = 2 e x = 3.
3. Vértice: (1, 1).
4. Gráfico com raízes x = -2 e x = 2, vértice (0, -4) e eixo de simetria x = 0.

5. Valor máximo: y = -2.
6. Altura máxima: 20 m, no tempo t = 2 s.
7. a) Coeficientes: a = 2, b = -8, c = 5. b) O sinal positivo de a indica uma concavidade voltada para cima.

8. a) Raízes: x = 2 e x = 5. b) Soma: 7. Produto: 10.

9. Número ideal de unidades: 2,5 (milhares). Lucro máximo: 15,5 (milhares).
10. Domínio: todos os números reais. Imagem: [0, +∞).

---

Atividade com Exercícios de Função Quadrática em PDF

Conclusão

Os exercícios propostos oferecem aos professores uma oportunidade de explorar as funções quadráticas de maneira prática e significativa em sala de aula. O uso de gráficos e problemas contextualizados ajuda os alunos a compreenderem melhor esse tema essencial, conectando-o a situações reais.

Veja mais Exercícios de Matemática para 9º Ano